Role of Stacks and Queues in Problem Solving

What is Stack & Queue ?

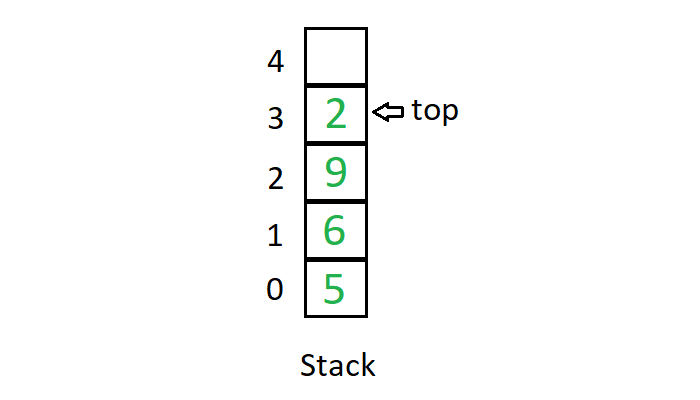
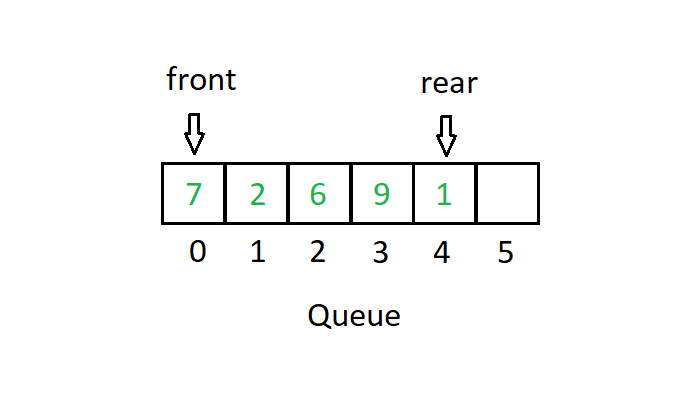
A stack is a linear data structure in which elements can be inserted and deleted only from one side of the list, called the top. and a queue is a linear data structure in which elements can be inserted only from one side of the list called rear, and the elements can be deleted only from the other side called the front.

Diagrammatic representation of stack

Diagrammatic representation of Queue

Difference Between Stack & Queue

1. Stacks are based on the LIFO principle, i.e., the element inserted at the last, is the first element to come out of the list & Queues are based on the FIFO principle, i.e., the element inserted at the first, is the first element to come out of the list.
2. Insert operation in Stack is called push operation & Insert operation in Queue is called enqueue operation.
3. In Stack Delete operation is called pop operation while In Queue Delete operation is called dequeue operation.
4. Stack is used in solving problems works on recursion & Queue is used in solving problems having sequential processing.

Applications of stack:

• Balancing of symbols.
• Infix to Postfix /Prefix conversion
• Redo-undo features at many places like editors, photoshop.
• Forward and backward feature in web browsers.

Applications of Queue:

• CPU scheduling, Disk Scheduling.
• Breadth First Search.
• Data transferring in two process Examples :IO Buffers, pipes, file IO, etc.

Demonstration of Stack Problem :

Balancing Parentheses:

This is very famous problem based on Stack.

First question came in our mind is where it is used?

The answer is it is used while writing the code in any programming language. Most of programming language need parentheses (brackets). If you write any mismatched bracket while coding then there must be an error.

The Next question is why to use Stack to solve this problem?

Can we use the simple logic like number of opening brackets is equal to number of closing brackets. But its wrong logic… For coding we have to write brackets in sequence and they should be balanced also.

Not Balanced Parentheses

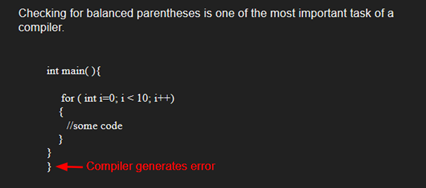
For example “( [ XYZ) ]” here in this example our previous logic condition is full filled but this is not a balanced. If you write like this example ,compiler will throw an error. So we have to use Stack to solve this problem.

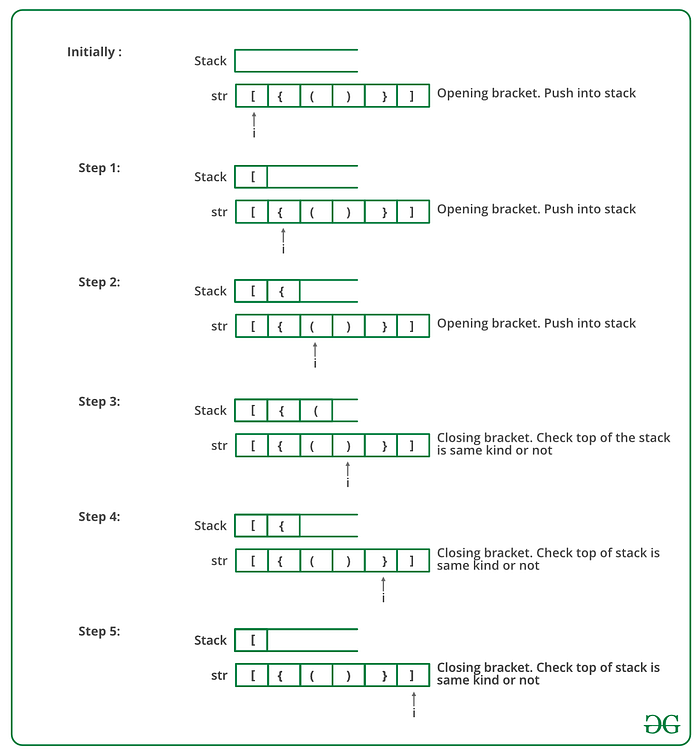
Algorithm:

• Declare a character stack S.
• Now traverse the expression string exp.

1. If the current character is a starting bracket (‘(‘ or ‘{‘ or ‘[‘) then push it to stack.
2. If the current character is a closing bracket (‘)’ or ‘}’ or ‘]’) then pop from stack and if the popped character is the matching starting bracket then fine else brackets are not balanced.
3. After complete traversal, if there is some starting bracket left in stack then “not balanced”

Below image is a dry run of the above approach:

So like this , we can use stack for Balancing Parentheses.